Is transience of a protocol shorter, if the mobility simulation is perfect ?
Example: DSR
The mobility model is restricted random-waypoint on Houston section. There are 50 mobiles. At a trip transition instant,
if phase is move, numerical speed is drawn at random, uniformly on the interval [0.01,9.99].
Else, if phase is pause, the duration of pause is drawn at random, uniformly on the interval [0,100].
The routing protocol is DSR. There are 20 data connections, each with a fixed packet send rate of 1 pkt/sec. Packet lengths are fixed to 512 B.
Default initilization rule : for each mobile, t=0 is a trip transition instant. Initially, each mobile is in move phase.
Results with no paussing are similar: see S. PalChaudhuri et al.
Numerical speed
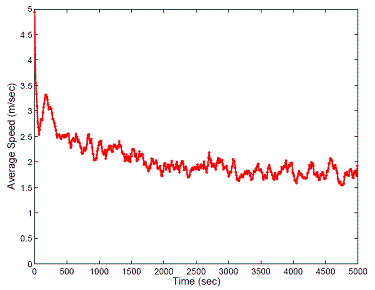
The left plot shows numerical speed averaged over all mobiles at time instants spanning [0,5000].
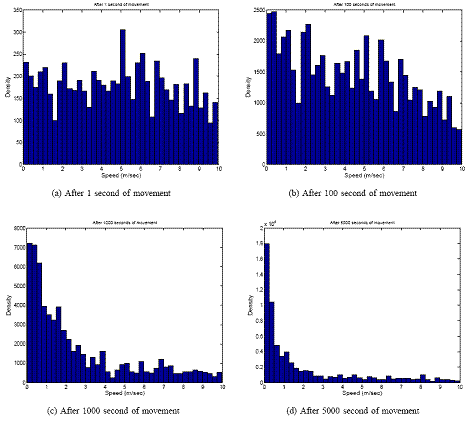
The right plots show histograms of mobile speeds at time 1, 100, 1000, and 5000 seconds since the simulation start.
Observations
- Initially, as t=0 is a trip transition instant, the speed is uniformly distributed on the interval [0.01,9.99]. Therein, its mean is 5.
- The distribution of numerical speed converges to that of unique steady-state distribution,
which is different than as seen at a trip transition instant.
- Visually, it takes more than 2000 seconds to converge !
Packet delivery ratio
The plots show packet delivery ratio defined as (# received packets) / (# transmitted packets), which is computed over 10-second intervals,
averaged over all data connections and averaged over 100 simulation runs.
|
With default initilization rule
|
 |
|
|
With perfect mobility simulation
|
 |
|
Check the hypothesis:
perfect simulation of mobility induces shorter transience for a protocol,
than with default initilization rule.
Back to main page